Decomposition and Visualization of Fourth-Order
Elastic-Plastic Tensors
Abstract:
Visualization of fourth-order tensors from solid mechanics has not
been explored in depth previously. Challenges include the
large number of components (3x3x3x3 for 3D), loss of major symmetry
and loss of positive definiteness (with possibly zero or negative eigenvalues).
This paper presents a decomposition of fourth-order tensors
that facilitates their visualization and understanding.
Fourth-order tensors are used to represent a solid's
stiffness. The stiffness tensor
represents the relationship between increments of stress and
increments of strain. Visualizing stiffness is important to
understand the changing state of solids during plastification
and failure. In this
work, we present a method to reduce the number of stiffness components to
second-order 3x3 tensors for visualization. The reduction is
based on polar decomposition, followed by eigen-decomposition on the
polar "stretch". If any resulting eigenvalue is significantly lower than
the others, the material has softened in that eigen-direction. The associated
second-order eigentensor represents the mode of stress (such as
compression, tension, shear, or some combination of these) to which the
material becomes vulnerable. Thus we can visualize the physical meaning of
plastification with techniques for visualizing second-order symmetric tensors.
Paper:
A
pdf
version of the paper is available.
Images:
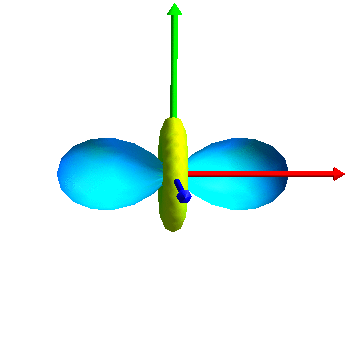
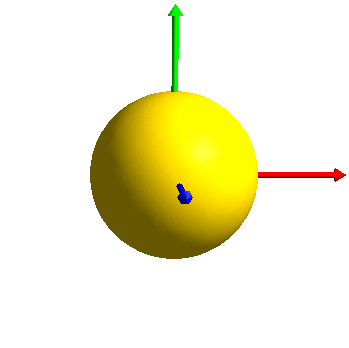
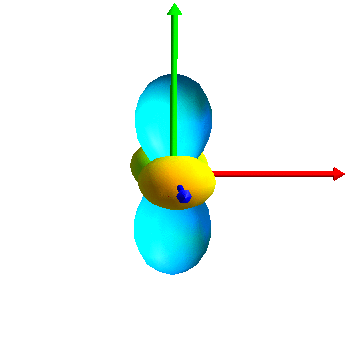
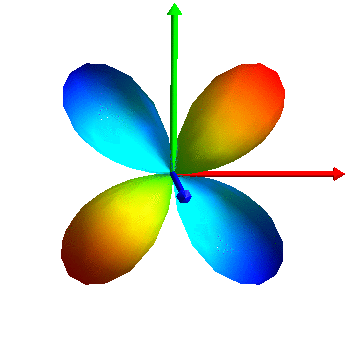
The 6 eigentensors:
 Return to AVIS home page.
Return to AVIS home page.