1
Computer Science Department, University of California, Santa Cruz
2
Department of Mathematics and Graduate School, University of California, Berkeley
Abstract:
Tensor topology is useful in providing a simplified and yet detailed
representation of a tensor field. Recently the field of 3D tensor topology
is advanced by the discovery that degenerate tensors usually form lines in
their most basic configurations.
These lines form the backbone for further topological analysis.
A number of ways for extracting and tracing the degenerate tensor lines
have also been proposed.
In this paper, we complete the previous work
by studying the behavior and extracting the separating surfaces
emanating from these degenerate lines.
First, we show that analysis of eigenvectors around
a 3D degenerate tensor can be reduced to 2D.
That is, in most instances,
the 3D separating surfaces are just the trajectory
of the individual 2D separatrices
which includes trisectors and wedges.
But the proof is by no means trivial since it is closely related to
perturbation theory around a pair of singular state.
Such analysis naturally breaks down at the tangential points
where the degenerate lines pass through the
plane spanned by the eigenvectors associated with the repeated eigenvalues.
Second, we show that the separatrices along a degenerate line
may switch types (e.g. trisectors to wedges)
exactly at the points where the eigenplane is tangential
to the degenerate curve.
This property leads to interesting and yet complicated configuration
of surfaces around such transition points.
Finally, we apply the technique to several common data
sets to verify its correctness.
Paper:
Download paper (pdf)
Images:
-
Random 3D Tensor Field:
This tensor field is obtained through trilinear interpolation of a single cell.
The corner values of this cell is generated randomly.
We use this method to generate a large number of data sets to verify our techniques.
Since this paper is the second installment of our last year's
TVCG paper,
we choose the same tensor field that also appeared in that paper for comparison.
The degenerate lines for this tensor field can be accessed
here.
The colormap for this data set is the actual integration length of the hypertreamline from
degenerate lines where it originates.
-
(Type L):

|

|

|

|

|
| (a)
| (b)
| (c)
| (d)
| (e)
|

|

|
| (f)
| (g)
|
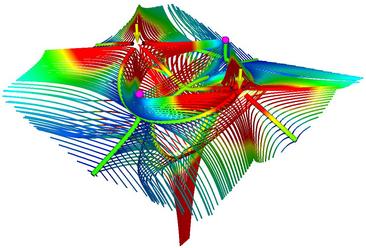
Figure 1. The Separating surfaces for minor hyperstreamlines.
They start from type-L degenerate lines.
There are three isolated pieces of degenerate lines in this tensor field:
a long winding line in the center and two shorter ones in two corners.
They can be seen clearly in (a).
If we walk from the bottom to the top on the central winding line,
we will experience a transition from single wedge points to trisectors.
The most interesting result is that one of the separating surface
goes below the degenerate line and wraps back to itself from the other side.
It can be seen clearly from (b) - (e).
(c) shows the seam that this separating surface connects back to itself.
(f) zooms in on one of the short lines.
This is a transition from double wedge points to trisectors.
(g) zooms in on the transition point on the long winding line.
-
(Type P):
Figure 2. The Separating surfaces for major hyperstreamlines.
They start from type-P degenerate lines.
There are two isolated type-P lines in this scene:
one long winding line in the center and one shorter one in the corner.
It can be seen from (a) and (b) that one of the separating surface
starting from the shorter line goes around the long winding line.
It is the red surface in the center. This forms the single wedge point pattern.
If we walk along the long winding line from the bottom to the top,
we will experience transitions from trisectors to double wedges
to single wedges to double wedges and then back to single wedges.
(d) shows the transition from trisectors to double wedges.
It is different from Figure 1(f) since the flipping separatrices
point to each other in this case.
So we see the separating surface actually wraps up on the same line.
It is an example of 3D separating surface interacting with the same degenerate
line that it originates.
(e) zooms in on the transition from single wedges to double wedges and
then back to single wedges again.
It it interesting to see that the separating surface is actually one
whole surface self-folded twice along the degenerate line.
-
Double Point Load Stress Tensors
This is a commonly used benchmark tensor field.
It is a stress tensor field from two points loads on a semi-infinite volume.
The two yellow arrows marks out the two points loads.
The two purple balls marks out the two triple degenerate points with
zero stress.
-
(Type L):
Figure 3. The Separating surfaces start from type-L degenerate lines.
There are altogether four isolated type-L degenerate lines in this data set.
(b) shows that their separating surface form interesting pattern
on the central surface that connects the two point loads.
(e) shows only the separating surface starting from the two bifurcated branches
directly below the point loads.
It is very interesting that the separating surface form a typical node (saddle)
shape structure.
-
(Type P):

|

|

|

|

|
| (a)
| (b)
| (c)
| (d)
| (e)
|

|

|
| (f)
| (g)
|
Figure 4. The Separating surfaces start from type-P degenerate lines.
There are altogether eight isolated type-P degenerate lines in this data set.
(a) - (e) shows all the separating surfaces but the ones starting from
the inner loop for visual clarity.
It is worth noticing that the separating surface form a bowl shape structure
in the middle.
(f) and (g) shows the separating surfaces starting from the inner loop structure.
In (f), if we walk on this inner loop structure from the top point along the
clock-wise direction for a full round, we will experience transitions from
single wedges to double wedges to trisectors to double wedges and then
back to single wedges again.
(g) zooms in on the location where the double wedges becomes the single wedges.
 Return to AVIS home page.
Return to AVIS home page.